Semana 1

Notas de clase de la semana 1 de LPP.

Tema 0: Presentación de la asignatura

Temario

Planificación

Horarios

Prácticas

Cuestionarios

Evaluación

Consejos para aprender con éxito

Cómo dominar los conceptos

Para superar la asignatura lo que hice fue estudiar mucho. Hay que practicar y sobre todo entender los ejercicios y no sabérselos de memoria. Una vez dominados los ejercicios yo mismo me propuse variantes de los mismos. Así es como se domina.

No copiar las prácticas

El mayor problema que creo que existe es que muchas personas se relajan y se copian las prácticas en cuanto les resultan un poco difíciles o les lleva algo mas del tiempo que les gustaría. Esta asignatura si no haces tu los ejercicios y te peleas con ellos es prácticamente imposible de sacar.

No memorizar

Otra de las cosas es que tienes que cambiar la forma de estudiar, no vale memorizar, ni hacer muchos ejercicios sin más. Tienes que entender bien el funcionamiento de la recursión para luego poder practicar con ejercicios, sino no sirve. [...] En mi opinión el problema de LPP para mucha gente es que para los exámenes se memorizan los ejercicios de prácticas de las soluciones que se dan en clase.

Tema 1: Lenguajes de programación.

Tema no presencial para estudiar en casa.

Algunos lenguajes importantes y su fecha de creación

1950-1960 1970 1980 1990 2000
1957 FORTRAN 1970 Pascal 1980 Smalltalk-80 1990 Haskell 2000 C#
1958 ALGOL 1972 Prolog 1983 Objective-C 1991 Python 2003 Scala
1960 Lisp 1972 C 1983 Ada 1993 Ruby 2003 Groovy
1960 COBOL 1975 Scheme 1986 C++ 1995 Java 2009 Go
1962 APL 1975 Modula 1986 Eiffel 1995 Racket 2014 Swift
1964 BASIC 1987 Perl
1967 SIMULA

Genealogía de los lenguajes de programación

Lista TIOBE

La lista TIOBE se publica cada año indicando los lenguajes de programación más populares.

Paradigmas de programación

Tema 2: Programación funcional

Veremos hoy

  1. El paradigma de Programación Funcional
  2. Scheme como lenguaje de programación funcional

Definición de programación funcional

Un programa funcional es

Un conjunto de funciones matemáticas que convierten unas entradas en unas salidas, sin ningún estado interno y ningún efecto lateral.

Principales características del paradigma funcional

Orígenes históricos

Historia y características del Lisp

Lenguajes de programación funcional

Lenguajes modernos principalmente funcionales:

Lenguajes multi-paradigma en los que se puede usar POO y PF:

Lenguaje funcional puro más importante:

Aplicaciones prácticas de la programación funcional

Evaluación de expresiones y definición de funciones

Evaluación de expresiones

2 ⇒ 2
(+ 2 3) ⇒ 5
(+) ⇒ 0
(+ 2 4 5 6) ⇒ 17
(+ (* 2 3) (- 3 1)) ⇒ 8

Se dice "evaluar una expresión" en lugar de "ejecutar una expresión".

Partes de una expresión:

Por ejemplo, ¿cuál es la evaluación de la siguiente expresión?:

(+ (* 2 3) (- 3 (/ 12 3)))

Definición de funciones

Definición

(define (cuadrado x)
   (* x x))

Uso y evaluación:

(cuadrado 10) ⇒ 100
(cuadrado (+ 10 (cuadrado (+ 2 4)))) ⇒ 2116

Definición de funciones auxiliares

(define (suma-cuadrados x y)
   (+ (cuadrado x) (cuadrado y)))

Funciones puras

Composición de funciones

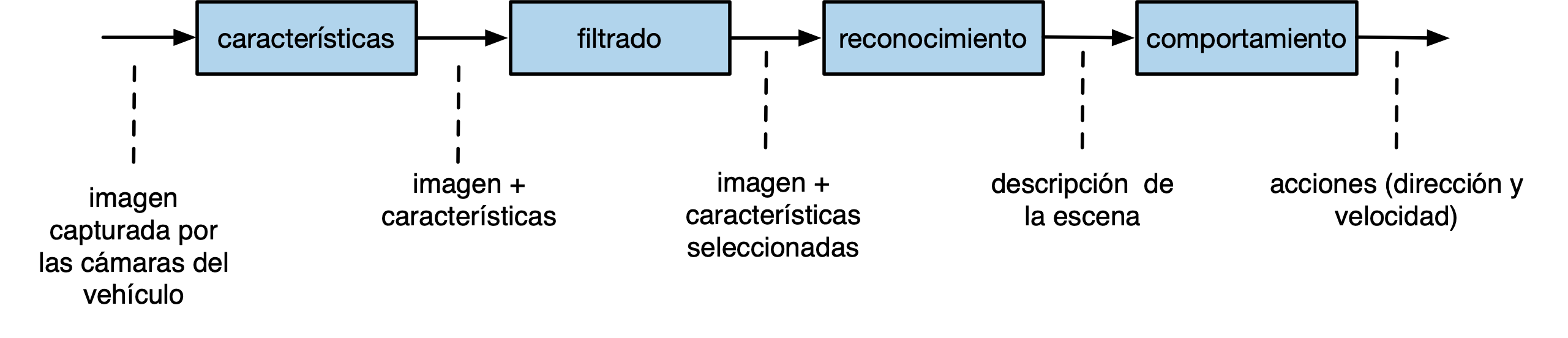
(define (conduce-vehiculo imagenes)
    (obten-acciones 
        (reconoce 
            (filtra 
                (obten-caracteristicas imagenes)))))

Programación declarativa

Otro ejemplo de programación declarativa: SwiftUI.

(define (cuadrado x)
   (* x x))

(cuadrado 4) ; devuelve 16

Programación imperativa

Características:

Pasos de ejecución

Pasos de ejecución en C:

int a = cuadrado(8);
int b = doble(a);
int c = cuadrado(b);
return c

En Swift:

filtrados = filtra(pedidos);
procesados = procesa(filtrados);
return procesados;

En programación funcional, en lugar de pasos de ejecución se utiliza como hemos visto la composición de funciones. Los ejemplos anteriores se expresan de la siguiente forma en programación funcional:

(cuadrado (doble (cuadrado 8)))

(procesa (filtra pedidos))

Mutación

Asignación destructiva o mutación:

int x = 10;
int x = x + 1;

En programación funcional los valores definidos son inmutables:

#lang racket

(define a 12)
(define a 200)

tendremos el siguiente error:

module: identifier already defined in: a

En lenguajes imperativos también hay sentencias declarativas:

1. int x = 1;   // declarativa
2. x = x+1;     // imperativa
3. int y = x+1; // declarativa
4. y = x;       // imperativa

Mutación y efectos laterales

Ejemplo de mutación:

Point2D p1 = new Point2D(3.0, 2.0); // la coord x de p1 es 3.0
p1.getCoordX(); // la coord x de p1 es 3.0
p1.setCoordX(10.0);
p1.getCoordX(); // la coord x de p1 es 10.0

Ejemplo de efecto lateral:

Point2D p1 = new Point2D(3.0, 2.0); // la coord x de p1 es 3.0
p1.getCoordX(); // la coord x de p1 es 3.0
Point2D p2 = p1;
p2.setCoordX(10.0);
p1.getCoordX(); // la coord x de p1 es 10.0, sin que ninguna sentencia haya modificado directamente p1

Estado local mutable

Función con estado local mutable en lenguaje imperativo (Java):

public class Contador {
    int c;

    public Contador(int valorInicial) {
        c = valorInicial;
    }

    public int valor() {
        c++;
        return c;
    }
}

Contador cont = new Contador(10);
cont.valor(); // 11
cont.valor(); // 12
cont.valor(); // 13

En C:

int function contador () {
    static int c = 0;

    c++;
    return c;
}

contador() ;; 1
contador() ;; 2
contador() ;; 3

Por el contrario, los lenguajes funcionales puros tienen la propiedad de transparencia referencial: si se sustituye una expresión por su valor el resultado final no debe cambiar. -> funciones no modifican estado.

Resumen

Características de la programación declarativa

Características de la programación imperativa

Programación funcional

Primeras características que vamos a ver hoy:

Modelo de computación de sustitución

Reglas del modelo de sustitución

  1. Si e es un valor primitivo (por ejemplo, un número), devolvemos ese mismo valor.
  2. Si e es un identificador, devolvemos su valor asociado con un define (se lanzará un error si no existe ese valor).
  3. Si e es una expresión del tipo (f arg1 ... argn), donde f es el nombre de una función primitiva (+, -, ...), evaluamos uno a uno los argumentos arg1 ... argn (con estas mismas reglas) y evaluamos la función primitiva con los resultados.

La regla 4 tiene dos variantes, dependiendo del orden de evaluación que utilizamos.

Orden aplicativo

  1. Si e es una expresión del tipo (f arg1 ... argn), donde f es el nombre de una función definida con un define, tenemos que evaluar primero los argumentos arg1 ... argn y después sustituir f por su cuerpo, reemplazando cada parámetro formal de la función por el correspondiente argumento evaluado. Después evaluaremos la expresión resultante usando estas mismas reglas.

Orden normal

  1. Si e es una expresión del tipo (f arg1 ... argn), donde f es el nombre de una función definida con un define, tenemos que sustituir f por su cuerpo, reemplazando cada parámetro formal de la función por el correspondiente argumento sin evaluar. Después evaluar la expresión resultante usando estas mismas reglas.
(define (doble x) 
    (+ x x))

(define (cuadrado y) 
    (* y y))

(define a 2)

(doble (cuadrado a))

Orden aplicativo:

(doble (cuadrado a)) ⇒       ; Sustituimos a por su valor (R2)
(doble (cuadrado 2)) ⇒       ; Sustitumos cuadrado por su cuerpo (R4)
(doble (* 2 2)) ⇒            ; Evaluamos (* 2 2) (R3)
(doble 4) ⇒                  ; Sustituimos doble por su cuerpo (R4)
(+ 4 4) ⇒                    ; Evaluamos (+ 4 4) (R3)
8

Orden normal:

(doble (cuadrado a)) ⇒            ; Sustituimos doble por su cuerpo (R4)
(+ (cuadrado a) (cuadrado a) ⇒    ; Sustituimos cuadrado por su cuerpo (R4)
(+ (* a a) (* a a)  ⇒             ; Sustitumos a por su valor (R2)
(+ (* 2 2) (* 2 2)  ⇒             ; Evaluamos (* 2 2) (R3)
(+ 4 (* 2 2))  ⇒                  ; Evaluamos (* 2 2) (R3)
(+ 4 4)  ⇒                        ; Evaluamos (+ 4 4) (R3)
8

Ejemplo de resultado distinto con funciones no puras:

(define (zero x) (- x x))
(zero (random 10))

Funciones y formas especiales en Scheme

Forma especial define

Sintaxis

(define <identificador> <expresión>)

Evaluación

  1. Evaluar expresión
  2. Asociar el valor resultante con el identificador

Ejemplo

(define base 10)   ; Asociamos a 'base' el valor 10
(define altura 12) ; Asociamos a 'altura' el valor 12
(define area (/ (* base altura) 2)) ; Asociamos a 'area' el valor 60

Forma especial define para definir funciones

Sintaxis

(define (<nombre-funcion> <argumentos>)
    <cuerpo>)

Evaluación

  1. Crear la función con el cuerpo
  2. Dar a la función el nombre nombre-función

Ejemplo

(define (factorial x)
    (if (= x 0)
        1
        (* x (factorial (- x 1)))))

Forma especial if

Sintaxis

(if <condición> <expresión-true> <expresión-false>)

Evaluación

  1. Evaluar condición
  2. Si el resultado es #t evaluar la expresión-true, en otro caso, evaluar la expresión-false

Ejemplo

(if (> 10 5) (substring "Hola qué tal" (+ 1 1) 4) (/ 12 0))

;; Evaluamos (> 10 5). Como el resultado es #t, evaluamos 
;; (substring "Hola qué tal" (+ 1 1) 4), que devuelve "la"

Forma especial cond

Sintaxis

(cond 
    (<exp-cond-1> <exp-consec-1>)
    (<exp-cond-2> <exp-consec-2>)
    ...
    (else <exp-consec-else>))

Evaluación

  1. Se evalúan de forma ordenada todas las expresiones hasta que una de ellas devuelva #t
  2. Si alguna expresión devuelve #t, se devuelve el valor del consecuente de esa expresión
  3. Si ninguna expresión es cierta, se devuelve el valor resultante de evaluar el consecuente del else

Ejemplo

(cond
   ((> 3 4) "3 es mayor que 4")
   ((< 2 1) "2 es menor que 1")
   ((= 3 1) "3 es igual que 1")
   ((> 3 5) "3 es mayor que 2")
   (else "ninguna condición es cierta"))

;; Se evalúan una a una las expresiones (> 3 4),
;; (< 2 1), (= 3 1) y (> 3 5). Como ninguna de ella
;; es cierta se devuelve la cadena "ninguna condición es cierta"

Forma especial quote y símbolos

Sintaxis

(quote <identificador>)
(quote <expresion>)

Evaluación

Ejemplo

(quote x) ; el símbolo x
'hola ; el símbolo hola
'(+ 1 2 3 4) ; la lista formada por el símbolo + y los números 1 2 3 4
(quote (1 2 3 4)) ; la lista formada por los números 1 2 3 4
'(* (+ 1 (+ 2 3)) 5) ; una lista con 3 elementos, el segundo de ellos otra lista

Ejemplos de funciones Scheme con símbolos:

(define x 12)
(symbol? 'x) ; ⇒ #t
(symbol? x) ; ⇒ #f ¿Por qué?
(symbol? 'hola-que<>)
(symbol->string 'hola-que<>)
'mañana
'lápiz ; aunque sea posible, no vamos a usar acentos en los símbolos
; pero sí en los comentarios
(symbol? "hola") ; #f
(symbol?  #f) ; #f
(symbol? (car '(hola cómo estás))) ; #t
(equal? 'hola 'hola)
(equal? 'hola "hola")

Un símbolo es un identificador que puede asociarse o ligarse (bind) a un valor (cualquier dato de primera clase).

Cuando escribimos un símbolo en el prompt de Scheme el intérprete lo evalúa y devuelve su valor:

(define pi 3.14159)
pi
⇒3.14159

Los nombres de las funciones (equal?,sin, `+, ...) son también símbolos (los de las macros no) y Scheme también los evalúa (en un par de semanas hablaremos de las funciones como objetos primitivos en Scheme):

sin
⇒ #<procedure:sin>
+
⇒ #<procedure:+>
(define (cuadrado x) (* x x))
⇒ #<procedure:cuadrado>

Símbolos como tipos primitivos

Los símbolos son tipos primitivos del lenguaje: pueden pasarse como parámetros o ligarse a variables.

(define x 'hola)
x
⇒ hola

Listas

Función list y forma especial quote

(list 1 2 3 4 5) ⇒ (1 2 3 4)
(list 'a 'b 'c) ⇒ (a b c)
(list 1 'a 2 'b 3 'c #t) ⇒ (1 a 2 b 3 c #t)
(list 1 (+ 1 1) (* 2 (+ 1 2))) ⇒ (1 2 6)

Otro ejemplo:

(define a 1)
(define b 2)
(define c 3)
(list a b c) ; ⇒ (1 2 3)

'(1 2 3 4) ; ⇒ (1 2 3 4)
(define a 1)
(define b 2)
(define c 3)
'(a b c) ; ⇒ (a b c)
'(1 (+ 1 1) (* 2 (+ 1 2))) ; ⇒ (1 (+ 1 1) (* 2 (+ 1 2)))

La última lista tiene 3 elementos:

(list 1 (/ 2 3) (+ 2 3)) ; ⇒ (1 2/3 5)

'(1 (/ 2 3) (+ 2 3)) ; ⇒ (1 (/ 2 3) (+ 2 3))

Selección de elementos de una lista: car y cdr

Ejemplos:

(define lista1 '(1 2 3 4))
(car lista1) ; ⇒ 1
(cdr lista1) ; ⇒ (2 3 4)
(define lista2 '((1 2) 3 4))
(car lista2) ; ⇒ (1 2)
(cdr lista2) ; ⇒ (3 4)

Composición de listas: cons y append

(cons 1 '(1 2 3 4)) ; ⇒ (1 1 2 3 4)
(cons 'hola '(como estás)) ; ⇒ (hola como estás)
(cons '(1 2) '(1 2 3 4))  ; ⇒ ((1 2) 1 2 3 4)

(define list1 '(1 2 3 4))
(define list2 '(hola como estás))
(append list1 list2) ; ⇒ (1 2 3 4 hola como estás)