Práctica 3: Recursión, parejas y diagramas box-and-pointer¶

Antes de la clase de prácticas¶

Antes de empezar esta práctica es importante que revises la solución de la práctica 2. Puedes preguntar las dudas al profesor de prácticas.
Los siguientes ejercicios están basados en los conceptos de teoría vistos la semana pasada. Antes de la clase de prácticas debes repasar todos los conceptos y probar en el DrRacket todos los ejemplos de los siguientes apartados del tema 2 Programación Funcional:
- 2.7 Recursión
- 2.8 Recursión y listas
- 3 Tipos de datos compuestos en Scheme
- 4 Listas en Scheme

Ejercicios¶

Abre el DrRacket y crea el fichero practica3.rkt en el que deberás escribir todos los ejemplos y soluciones de los ejercicios que hagas.

Función auxiliar para dibujar diagramas caja y puntero¶

Descarga el fichero lpp.rkt, pulsando el botón derecho del ratón y seleccionando la opción Guardar como lpp.rkt. Guárdalo en la misma carpeta en la que tengas el fichero practica3.rkt. Contiene la definición de una función auxiliar (caja-puntero dato) que te permite crear diagramas caja y puntero de estructuras de parejas.

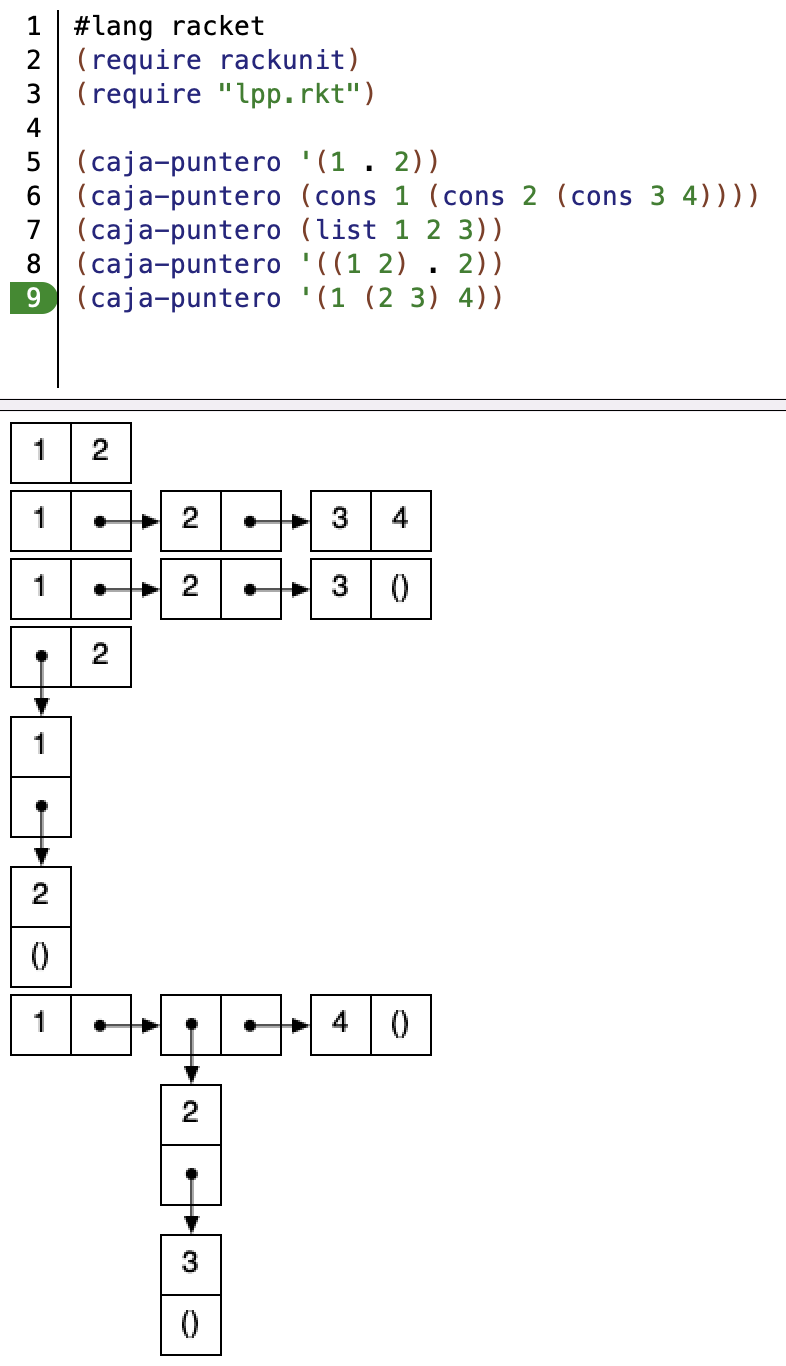
El siguiente programa muestra un ejemplo del uso de esta función:

#lang racket
(require rackunit)
(require "lpp.rkt")

(caja-puntero '(1 . 2))
(caja-puntero (cons 1 (cons 2 (cons 3 4))))
(caja-puntero (list 1 2 3))
(caja-puntero '((1 2) . 2))
(caja-puntero '(1 (2 3) 4))

La siguiente imagen muestra la ejecución del programa en el DrRacket.

Puedes mirar el código fuente del fichero lpp.rkt para curiosear cómo está implementada la función caja-puntero. Se utiliza la librería de imágenes de Racket 2htdp/image.

Para usar la librería hay que incluir la siguiente línea en nuestro programa:

#lang racket
(require 2htdp/image)

Una cosa muy interesante de esta librería es que define las imágenes como objetos de primera clase del lenguaje, que pueden asignarse a variables o pasarse como parámetro para construir otras imágenes. Lo podemos ver en el siguiente ejemplo:

Incluso podemos incluir imágenes en listas:

Ejercicio 1¶

a.1) Implementa la función recursiva (minimo lista) que recibe una lista con números como argumento y devuelve el menor número de la lista. Suponemos listas de 1 o más elementos.

Para la implementación debes usar la función menor definida en la práctica anterior.

Pista

Podemos expresar el caso general de la recursión de la siguiente forma:

El mínimo de los elementos de una lista es el menor entre el primer elemento de la lista y el mínimo del resto de la lista.

Y el caso base:

El mínimo de una lista con un único número es ese número.

Ejemplos:

(minimo '(2)) ; ⇒ 2
(minimo '(1 8 6 4 3)) ; ⇒ 1
(minimo '(1 -1 3 -6 4)) ; ⇒ -6

Cómo comprobar el caso base de minimo

Para el caso base de la función minimo debemos comprobar si la lista que recibimos tiene un solo elemento. En ese caso el mínimo de la lista es el propio elemento. Sería un error llamar a la recursión porque no se puede calcular el menor elemento de una lista vacía.

La mejor forma de comprobar en Scheme si una lista tiene un solo elemento es:

(null? (rest lista))

Esta forma es más eficiente que llamar a la función length que necesita recorrer toda la lista. El coste de la instrucción (null? (rest lista)) no depende de la longitud de la lista, es O(1). Sin embargo, la instrucción (length lista) tiene que recorrer toda la lista por lo que tiene una complejidad de O(n).

Muchas veces verás también una expresión equivalente para comprobar si una lista tiene un único elemento: :

(null? (cdr lista))

Es una expresión que suelen usar los programadores de Scheme, algo que se conoce como una expresión idiomática del lenguaje.

a.2) Vamos a investigar el funcionamiento de la recursión en la función minimo. Supongamos la siguiente llamada:

(minimo '(1 8 6 4 3)) ; ⇒ 1

¿Qué lista se pasa como parámetro a la primera llamada recursiva a la función?
¿Qué devuelve esa llamada recursiva?
¿Con qué argumentos se llama a la función menor que devuelve el resultado final?

b) Implementa la función recursiva (concatena lista-chars) que recibe una lista de caracteres y devuelve la cadena resultante de concatenarlos.

Ejemplos:

(concatena '()) ; ⇒ ""
(concatena '(#\H #\o #\l #\a)) ; ⇒ "Hola"
(concatena '(#\S #\c #\h #\e #\m #\e #\space #\m #\o #\l #\a))  
; ⇒ "Scheme mola"

c) Implementa la función recursiva (cifra-cadena cad desplazamiento) que, usando la función cifra-caracter de la práctica anterior, cifre una cadena completa usando el cifrado de César.

Implementa después la función (descifra-cadena cad desplazamiento) que descifra una cadena completa.

Ejemplos:

(cifra-cadena "En un lugar de la Mancha, de cuyo nombre no quiero acordarme" 10) ; ⇒
"Ox ex veqkb no vk Wkxmrk, no meiy xywlbo xy aesoby kmybnkbwo"

(descifra-cadena "Ox ex veqkb no vk Wkxmrk, no meiy xywlbo xy aesoby kmybnkbwo" 10) ; ⇒
"En un lugar de la Mancha, de cuyo nombre no quiero acordarme"

d) Implementa el predicado recursivo (contiene? lista elemento) que comprueba si una lista tiene un elemento determinado. Después úsala para implementar la función (str-contiene? cadena char) que comprueba si una cadena contiene un carácter. Recuerda que la función string->list que convierte una cadena en una lista de caracteres.

Ejemplos:

(contiene? '(algo 3 #\A) 3) ; ⇒ #t
(contiene? '(algo 3 #\A) "algo") ; ⇒ #f
(contiene? '(algo 3 #\A) 'algo) ; ⇒ #t
(str-contiene? "Hola" #\o) ; ⇒ #t
(str-contiene? "Esto es una frase" #\space) ; ⇒ #t
(str-contiene? "Hola" #\h) ; ⇒ #f

Ejercicio 2¶

a) Implementa el predicado recursivo (todos-iguales? lista) que comprueba si todos los elementos de una lista son iguales.

(todos-iguales? '()) ; ⇒ #t
(todos-iguales? '(a)) ; ⇒ #t
(todos-iguales? '(a a a a a a a)) ; ⇒ #t
(todos-iguales? '((a b) (a b) (a b))) ; ⇒ #t
(todos-iguales? '(a a a a a b)) ; ⇒ #f

b) Implementa el predicado recursivo (todos-distintos? lista) que comprueba si todos los elementos de una lista son distintos. Para su implementación debes usar el predicado del ejercicio 1 contiene?.

(todos-distintos? '()) ; ⇒ #t
(todos-distintos? '(a)) ; ⇒ #t
(todos-distintos? '(a b c)) ; ⇒ #t
(todos-distintos? '(a b c a)) ; ⇒ #f

c) Implementa el predicado recursivo (solo-dos-iguales? lista)que comprueba que solo hay dos elementos iguales en una lista (los únicos elementos repetidos que hay en la lista se repiten dos veces). Para su implementación puedes usar los predicados anteriores.

(solo-dos-iguales? '()) ; ⇒ #f
(solo-dos-iguales? '(a)) ; ⇒ #f
(solo-dos-iguales? '(a b c a)) ; ⇒ #t
(solo-dos-iguales? '(a b c b a a)) ; ⇒ #f
(solo-dos-iguales? '(a b c a a)) ; ⇒ #f
(solo-dos-iguales? '(a b c a b)) ; ⇒ #f

Ejercicio 3¶

a.1) Dado el siguiente box & pointer, escribe la expresión en Scheme que define p1 usando el mínimo número de llamadas a list y cons. No debes utilizar expresiones con quote para construir las listas ni las parejas. Puedes usar la función gráfica caja-puntero para comprobar si tu solución es correcta.

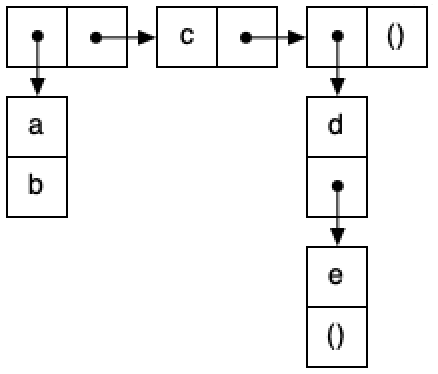
a.2) Escribe las expresiones que devuelven b y d a partir de p1. Debes usar las funciones sobre listas first, second, etc. si el argumento es una lista y car y cdr si es una pareja que no forma parte de una lista.

b.1) Dado el siguiente diagrama caja y puntero, escribe la expresión en Scheme que define p2 usando el mínimo número de llamadas a list y cons.

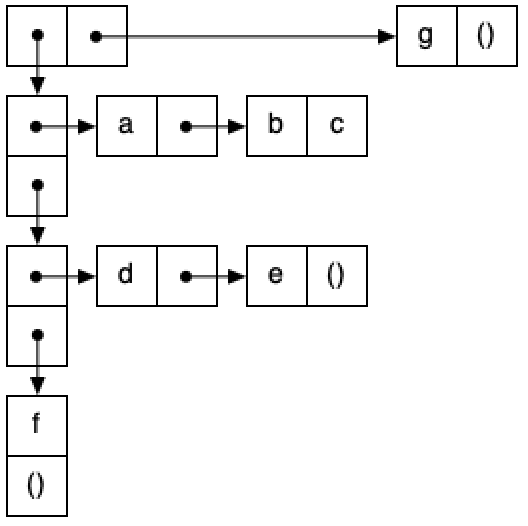
b.2) Escribe las expresiones que devuelven c y e a partir de p2. Debes usar las funciones sobre listas first, second, etc. si el argumento es una lista y car y cdr si es una pareja que no forma parte de una lista.

Ejercicio 4¶

Implementa la función recursiva (contar-datos-iguales lista-parejas) que recibe una lista de parejas y devuelve el número de parejas que tienen sus dos datos iguales.

(contar-datos-iguales '((2 . 3) ("hola" . "hola") (\#a . \#a) (true . false))) ; ⇒ 2
(contar-datos-iguales '((2 . "hola") ("hola" . 3) (\#a . true) (\#b . false))) ; ⇒ 0

Ejercicio 5¶

Vamos a seguir jugando al poker. Esta vez vamos a definir funciones sobre manos de cartas, definidas como listas de 5 símbolos que representan cartas.

Por ejemplo, las siguientes manos:

(define mano1 '(A♦ 2♦ 3♣ 4♦ 5♥))
(define mano2 '(J♦ J♣ J♠ J♥ K♣))

Copia de la práctica anterior la solución de la función (valor-carta carta) que devuelve el valor numérico de una carta:

(valor-carta '5♣) ; ⇒ 5
(valor-carta 'K♦) ; ⇒ 12

a) Implementa la función (palo-carta carta) de forma similar a la función valor-carta para que devuelva el símbolo con la descripción del palo de la carta.

(palo-carta 'A♠) ; ⇒ Picas
(palo-carta '2♣) ; ⇒ Tréboles
(palo-carta '3♥) ; ⇒ Corazones
(palo-carta '4♦) ; ⇒ Diamantes

Tendrás que usar las funciones valor-carta y palo-carta para implementar las siguientes funciones del ejercicio.

b) Implementa la función recursiva (veces-palo lista palo) que devuelve el número de veces que aparece un palo en una lista de cartas.

(veces-palo '(5♠ 6♣ 7♥ 8♦ 9♠) 'Picas) ; ⇒ 2
(veces-palo '(J♠ Q♣ K♥) 'Diamantes) ; ⇒ 0
(veces-palo '(A♣ 2♥ 3♠) 'Corazones) ; ⇒ 1
(veces-palo '() 'Tréboles) ; ⇒ 0

Usando la función anterior, implementa el predicado color? que comprueba si en una mano tenemos todas las cartas del mismo palo:

(color? '(5♣ J♦ J♣ Q♠ Q♥)) ; ⇒ #f
(color? '(2♦ 5♦ 6♦ J♦ K♦)) ; ⇒ #t

c) Implementa el predicado recursivo escalera? que recibe una lista de cartas y comprueba si todas ellas tienen valores consecutivos, ordenados de menor a mayor.

(escalera? '(5♣ 4♦ 3♣)) ; ⇒ #f
(escalera? '(8♣ 9♦ J♣ Q♦)) ; ⇒ #t
(escalera? '(8♣ 2♣)) ; ⇒ #f
(escalera? '(A♣ 2♦ 3♣)) ; ⇒ #t

Usando las funciones anteriores implementa la función (escalera-color? mano) que comprueba si una mano de cartas es una escalera de color. Suponemos que las cartas que forman la mano están ordenadas de menor a mayor.

(escalera-color? '(5♣ 6♦ 7♣ 8♠ 9♥)) ; ⇒ #f
(escalera-color? '(A♦ 2♦ 3♦ 4♦ 5♦)) ; ⇒ #t

Ejercicio 6¶

a) Implementa las funciones (suma-izq pareja n) y (suma-der pareja n) definidas de la siguiente forma:

(suma-izq pareja n): devuelve una nueva pareja con la parte izquierda incrementada en n.
(suma-der pareja n): devuelve una nueva pareja con la parte derecha incrementada en n.

Ejemplos:

(suma-izq (cons 10 20) 3)  ; ⇒ (13 . 20)
(suma-der (cons 10 20) 5)  ; ⇒ (10 . 25)

b) Implementa la función recursiva (suma-impares-pares lista-num) que devuelva una pareja cuya parte izquierda sea la suma de los números impares de la lista y la parte derecha la suma de los números pares. Debes utilizar las funciones auxiliares definidas en el apartado anterior. También puedes utilizar las funciones predefinidas even? y odd?.

Ejemplos:

(suma-impares-pares '(3 2 1 4 8 7 6 5)) ; ⇒ (16 . 20)
(suma-impares-pares '(3 1 5))           ; ⇒ (9 . 0)

c) Implementa la función recursiva (cadena-mayor lista) que recibe un lista de cadenas y devuelve una pareja con la cadena de mayor longitud y dicha longitud. En el caso de que haya más de una cadena con la máxima longitud, se devolverá la última de ellas que aparezca en la lista.

En el caso en que la lista sea vacía se devolverá la pareja con la cadena vacía y un 0 (la longitud de la cadena vacía).

Pista: puedes utilizar la función string-length

(cadena-mayor '("vamos" "a" "obtener" "la" "cadena" "mayor")) ; ⇒  ("obtener" . 7)
(cadena-mayor '("prueba" "con" "maximo" "igual")) ; ⇒ ("maximo" . 6)
(cadena-mayor '()) ; ⇒ ("" . 0)

Lenguajes y Paradigmas de Programación, curso 2023-24
© Departamento Ciencia de la Computación e Inteligencia Artificial, Universidad de Alicante
Domingo Gallardo, Cristina Pomares, Antonio Botía, Francisco Martínez